ejemplo de linea de espera

Linea de Espera

Una línea de espera es el efecto resultante en un sistema cuando la demanda de un servicio supera la capacidad de proporcionar dicho servicio. Este sistema está formado por un conjunto de entidades en paralelo que proporcionan un servicio a las transacciones que  aleatoriamente entran al sistema. Dependiendo del sistema que se trate, las entidades  pueden ser cajeras, máquinas, semáforos, grúas, etcétera, mientras que las transacciones pueden ser: clientes, piezas, autos, barcos, etcétera. Tanto el tiempo de servicio como las  entradas al sistema son fenómenos que generalmente tienen asociadas fuentes de variación  que se encuentran fuera del control del tomador de decisiones, de tal forma que se hace necesaria la utilización de modelos estocásticos que permitan el estudio de este tipo de sistemas.

Una línea de espera puede modelarse como un proceso estocástico en el cual la variable aleatoria se define como el número de transacciones en el sistema en un momento dado; el conjunto de valores que puede tomar dicha variable es {O, 1, 2, . . . , N\ y cada uno de ellos tiene asociada una probabilidad de ocurrencia.

Objetivo

El objetivo es determinar qué nivel de servicio, ya sea por cantidad de entidades o por la velocidad de ellas, proporcionar para minimizar el costo total del sistema. Este costo está formado tanto por costo de servicio como por el que causa la espera.

Estructura de un sistema de línea de espera

Línea de espera de un solo canal

Cada cliente debe pasar por un canal, una estación para tomar y surtir el pedido, para colocar el pedido, pagar la cuenta y recibir el producto. Cuanto llegan más clientes forman una línea de espera y aguardan que se desocupe la estación para tomar y surtir el pedido.

Modelo de línea de espera y programación lineal

Distribución de llegadas

Para determinar la distribución de probabilidad para la cantidad de llegadas en un período dado, se puede utilizar la distribución de Poisson.

/= Media o cantidad promedio de ocurrencia en un intervalo

e= 2.17828

X= cantidad de ocurrencias en el intervalo

Modelo de línea de espera y programación lineal

El tiempo de servicio es el tiempo que pasa un cliente en la instalación una vez el servicio ha iniciado.

Se puede utilizar la distribución de probabilidad exponencial para encontrar la probabilidad de que el tiempo de servicio sea menor o igual que un tiempo t.

e= 2.17828

μ= cantidad media de unidades que pueden servirse por período

Modelo de línea de espera y programación lineal

Disciplina de la línea de espera

Manera en la que las unidades que esperan el servicio se ordenan para recibirlo.

El primero que llega, primero al que se le sirve

Último en entrar, primero en salir

Atención primero a la prioridad más alta

Operación de estado estable

Generalmente la actividad se incrementa gradualmente hasta un estado normal o estable. El período de comienzo o principio se conoce como período transitorio, mismo que termina cuando el sistema alcanza la operación de estado estable o normal.

Modelos de línea de espera de un solo canal con llegadas de poisson y tiempos de servicio exponenciales

A continuación, las fórmulas que pueden usarse para determinar las características operativas de estado estable para una línea de espera de un solo canal.

El objetivo de las fórmulas es mostrar cómo se puede dar información acerca de las características operativas de la línea de espera.

Modelo de línea de espera y programación lineal

¿Cómo se puede mejorar la operación de línea de espera?

Características operativas para el sistema con la tasa media de servicio aumentada a μ=1.25 clientes por minuto.

Modelo de línea de espera y programación lineal

Modelo de línea de espera y programación lineal

Modelo de línea de espera y programación lineal

Análisis económico de las líneas de espera

Antes de que pueda llevarse a cabo un análisis económico de una línea de espera, debe elaborarse un modelo de costo total, el cual incluye el costo de esperar y el costo de servicio.

Cw= costo de esperar por período para cada unidad

L= cantidad promedio de unidades en el sistema

Cs= costo de servicio por período para cada canal

K= cantidad de canales

La forma general de las curvas de costo en el análisis económico de las líneas de espera consiste en que el costo del servicio aumenta conforme aumenta la cantidad de canales; pero con más canales, el servicio es mejor. Como resultado, el tiempo de espera y el costo disminuyen conforme se aumenta la cantidad de canales. Puede encontrarse la cantidad de canales que proporcionará una buena aproximación al diseño de costo total mínimo evaluando el costo total para varias alternativas de diseño.

Modelo de línea de espera y programación lineal

Teoría de inventarios

INVENTARIOS

Los Inventarios representan un importante factor de control para el flujo operativo de una actividad. Estos existen debido al hecho de que NO hay una respuesta inmediata de los suministros por parte de los proveedores, que garanticen una dinámica estable en la Cadena Logística. Esta última, encierra en un todo, cada una de las operaciones fundamentales de una empresa, desde la obtención de la Materia prima, fabricación y almacenamiento, hasta la distribución del producto final a los mercados. Pero, ¿cómo atribuir inventarios a cada uno de estos procesos?

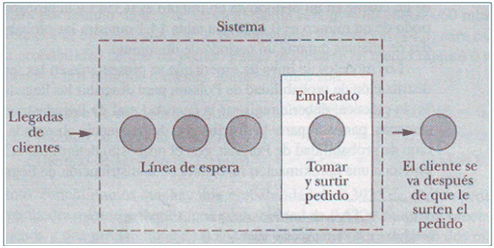
A continuación se muestra un esquema que simplifica lo explicado anteriormente, además de relacionar cada subdivisión de la Cadena Logística con sus correspondientes Inventarios:

Como podemos apreciar, cada eslabón de la cadena genera por cuenta propia un tipo de inventario diferente. Por este simple hecho, se hace indispensable desarrollar una visión crítica al estudio de los inventarios, así como de las principales ventajas y desventajas que ello conlleva. De esta forma entramos a analizar los diferentes Modelos utilizados para este fin, no sin antes dar unos conceptos previos:

Demanda: es el consumo en un determinado tiempo, también conocido como Potencial de Consumo.

Consumo: es la sumatoria de todas las demandas históricas de un período prolongado de tiempo.

En el estudio de los modelos se tendrá en cuenta principalmente el concepto de Demanda, debido al hecho de que es esta la que determina el comportamiento de los inventarios en un período de tiempo específico. Además de ello, para describir los modelos se debe hacer hincapié en el tipo de demanda, ya sea dependiente, si se tiene en cuenta la cantidad por pedido, o si es independiente, si las cantidades dependen de las demandas independientes, es decir, netamente aquellos que salen de los requerimientos del mercado (Necesidades), que a su vez no se saben cuáles son a ciencia cierta. Estas últimas pueden ser constantes y variables. Los siguientes son los Modelos de Inventario más importantes según la Demanda:

>> CON DEMANDA INDEPENDIENTE CONSTANTE:

• EOQ (Economic Order Quatity o Cantidad de Pedido Económica), esta a su vez se encuentra divida en:

- Sin Faltantes

- Con Faltantes

- Con Descuento por Volumen

• LEP (Lote Económico de Pedido), este puede ser también:

- Sin Faltantes

- Con Faltantes

>> CON DEMANDA INDEPENDIENTE VARIABLE:

• EOQ con Demanda Probabilística o estocástica.
• Simulación.
• Revisión, este puede ser a su vez:

- Periódicos: SISTEMA P

- Cantidades: SISTEMA Q

• Heurístico, sobresalen de este los conocidos AMORTIGUADORES (BUFFERS) relacionado a la DMB ( Dynamic Management of Buffer).

>> CON DEMANDA DEPENDIENTE:

• MRP I y II (Material Requirement Plan o Plan de Requerimiento de Material).

El Objetivo fundamental de estos modelos es: determinar con qué frecuencia y en qué cantidad reabastecer el Inventario, de manera que se minimicen los costos (o sumas de costos) por unidad de tiempo.

MODELOS DE INVERIO

<<EOQ SIN FALTANTES>>

Para el desarrollo de este modelo se tienen en cuenta varios supuestos:

1. La Demanda es constante, es decir que se conoce la tasa de demanda.
2. No se admiten faltantes.
3. Se le atribuye un costo por mantener guardado, es decir un costo por inventario.
4. Tiene un costo de Pedido.
5. Todos los costos se mantienen constantes.
6. La reposición es instantánea, esto es que NO existe un tiempo en el que el pedido se demora, es decir se reabastece inmediatamente cuando este llega a cero.

Bajo estos supuestos se puede graficar de la siguiente forma:

En donde Q es la cantidad o inventario máximo por pedido, D la demanda y t es la cantidad por demanda en un tiempo específico. Por otro lado, el área sombreada representa el costo en que se incurre por mantener guardado cierta cantidad de productos en un tiempo dado. Este a su vez varía según los períodos, por lo cual se determina un promedio que involucre a todos estos.

Es importante determinar los costos en los cuales se incurre por realizar dicha actividad, ya que, son estos los que nos van a proporcionar la información relevantes para la toma de decisiones. Para evaluar esto con base en el modelo EOQ, se hace referencia a laFunción de Costo de un pedido, la cual determina un Costo en función de las cantidades que consume la demanda en un período. La función está definida como:

Donde Cu representa los costos de adquisición, Cp los costos por hacer un pedido yC_MI los costos de inventario.

Además de ello, se debe hacer mención al número de períodos que se hacen en un tiempo, relacionado más que todo, al consumo en un lapso de tiempo prolongado, por ejemplo, un año. Entonces:

Para lo cual N es el número de períodos.

Lo anterior nos permite analizar el comportamiento de los costos asumidos por la actividad en períodos extensos. Con base en el modelo EOQ, donde nuestra única variable independiente es la Cantidad, podemos determinar un Costo total, multiplicando la Función de pedido por N. Así para un caso en concreto tendremos que el Costo Total Anual por pedidos CTA(Q) es:

Ahora bien, la relevancia de estos modelados matemáticos no es tan sólo determinar el costo total de la actividad, se debe pretender encontrar una solución óptima que mejor satisfaga nuestras expectativas como productores. En este caso, se debe optimizar la función con el propósito de Minimizar los costos y así obtener los mayores beneficios.Para esto se debe derivar la función CTA (Q) con respecto a las cantidades Q, igualando a cero y despejándola para obtener la cantidad óptima que se debe tener en inventario.

Despejando Q:

Donde Q* representa la cantidad óptima, y depende principalmente de Cp y C_MI. Con respecto a esto se deben hacer las siguientes consideraciones:

1. Cuando la cantidad que se elige es MENOR que la óptima, se puede apreciar que los costos de mantener en inventarios son menores que los generados por los costos por pedido. Esto es:

Cp > C_MI

2. Si se elige la cantidad óptima se igualan los costos de inventario y de pedido.

Cp = C_MI

3. Si se elige una cantidad MAYOR los costos por pedido tienden a ser menores que los generados por los inventarios.

Cp < C_MI



<<EOQ CON FALTANTES>>

Este modelo considera los mismos supuesto que el modelo EOQ Sin faltante, en lo único que difiere es que éste SI admite faltantes. En este caso se supone que el productor no puede abastecer completamente a la demanda en un período específico de tiempo, y para esto pide una extensión del plazo a los consumidores mientras se vuelve a abastecer (llenar el inventario), si este último acepta la prórroga de la entrega de su mercancia, debemos actuar bajo los preceptos del Modelo EOQ Con Faltantes.

A continuación se muestra la interpretación gráfica de este modelo.

A este tipo de Modelo se atribuyen costos igualmente por adquisición, por pedidos, por inventario, pero además de ellos también se entra a considerar un costo por faltantes denotado como Cf. No obstante, en la gráfica se aprecia que despejar todo en función de la cantidad Q no es la manera más apropiada para hallar la función de Costos de un pedido en un período, para esto se debe trabajar en función de las variables Q y S,tenemos que la función está dada por:

Donde Imáx es el inventario máximo en un solo período. Así mismo, a partir de la gráfica podemos deducir las siguientes relaciones:

Teniendo en cuenta lo anterior, reemplazamos en la función de costos de un pedido obteniendo:

Asimismo, multiplicando esta expresión por N podemos determinar el Costo total en un tiempo prolongado, por ejemplo anual. Esto es:

Como lo que verdaderamente nos interesa es encontrar las cantidades de Q y Sóptimas (las que generen los costos mínimos en cada caso), debemos determinar a partir de las derivadas parciales de cada variable independiente igualada a cero, un sistema de ecuaciones para hallarlas en dicho escenario óptimo. Tendremos que:

Desarrollando (2) con (2Q^2) como mínimo común denominador, así como Q y (Q-S) de (1) de nos queda:

Reemplazando Q y (Q-S) en (3) podemos despejar nuestra S óptima, la cual está dada por:

Reemplazando la S* hallada podemos calcular nuestra Q óptima, dada por:

<<LEP SIN FALTANTES (LOTE ECONÓMICO DE PRODUCCIÓN)>>

Para este modelo siguen los mismo supuestos, volvemos con la consideración de NOaceptar faltantes. En este caso, se tendrá en cuenta una rata de producción (R) que no es más que el promedio de unidades producidas en un período específico, la cual se mantiene constante. Además, dicha rata de producción es mayor que la demanda en dicho período, por lo cual cuando se satisface a esta última quedan sobrantes en inventario. En este momento no se asumira un costo de adquisición a menos que se acaben las existencias. Esto sucede periódicamente. En la siguiente gráfica puede verse el compartamiento de las existencias a través del tiempo.

Deduciendo de la gráfica tendremos que:

En este modelo, se hace referencia a los niveles de producción, entonces se hablará de costos por Orden de Producción (Cop) como aquel que repercute por mandar a fabricar una cantidad dada de producto en vez de lo que se consideraba como costo de pedido en los modelos previos. Teniendo en cuenta esto, tenemos que el Costo total en un período está dado por:

No obstante, considerando todo en función de la variable Q tendremos que deducir de la gráfica que:

Reemplazando en la función de Costo total de un período:

De la misma forma como hemos trabajado, calculamos la función de Costo Total en un período prolongado, por ejemplo anualmente, y tendremos que:

Asimismo procedemos a determinar la cantidad óptima Q* a partir de la función CTA, para esto derivamos, igualamos a cero y despejamos la variable señalada. Esto es:

<<LEP CON FALTANTES>>

Este modelo considera los mismos supuesto que el modelo EOQ Sin faltante, en lo único que difiere es que éste SI admite faltantes. En este caso se supone que el productor no puede abastecer completamente a la demanda en un período específico de tiempo, y para esto pide una extensión del plazo a los consumidores mientras se vuelve a abastecer (llenar el inventario), si este último acepta la prórroga de la entrega de su mercancia, debemos actuar bajo los preceptos del Modelo EOQ Con Faltantes.

A continuación se muestra la interpretación gráfica de este modelo.

A este tipo de Modelo se atribuyen costos igualmente por adquisición, por pedidos, por inventario, pero además de ellos también se entra a considerar un costo por faltantes denotado como Cf. No obstante, en la gráfica se aprecia que despejar todo en función de la cantidad Q no es la manera más apropiada para hallar la función de Costos de un pedido en un período, para esto se debe trabajar en función de las variables Q y S,tenemos que la función está dada por:

Donde Imáx es el inventario máximo en un solo período. Así mismo, a partir de la gráfica podemos deducir las siguientes relaciones:

Teniendo en cuenta lo anterior, reemplazamos en la función de costos de un pedido obteniendo:

Asimismo, multiplicando esta expresión por N podemos determinar el Costo total en un tiempo prolongado, por ejemplo anual. Esto es:

Como lo que verdaderamente nos interesa es encontrar las cantidades de Q y Sóptimas (las que generen los costos mínimos en cada caso), debemos determinar a partir de las derivadas parciales de cada variable independiente igualada a cero, un sistema de ecuaciones para hallarlas en dicho escenario óptimo. Tendremos que:

Desarrollando (2) con (2Q^2) como mínimo común denominador, así como Q y (Q-S) de (1) de nos queda:

Reemplazando Q y (Q-S) en (3) podemos despejar nuestra S óptima, la cual está dada por:

Reemplazando la S* hallada podemos calcular nuestra Q óptima, dada por:

<<MODELO EOQ CON DESCUENTOS POR CANTIDADES>>

Hasta este momento se han analizado los costos en que se incurre por pedir o por producir con una demanda constante, ya sea permitiendo o no faltantes en nuestros parámetros de inventario; asumiendo además que para el caso de producir la rata de producción debe ser mayor que la demanda del período. Esto dejando a un lado el efecto del costo unitario que se mantiene fijo en el tiempo y no varía si hay alguna modificación en la cantidad a pedir o producir. Dicho efecto no debe dejarse a un lado, ya que muchas empresas trabajan bajo este criterio, siempre, cuando se varía el nivel de pedido habrá un descuento adicional sobre el costo del mismo. Es por esto que a continuación se hablará acerca del Modelo EOQ con Descuento por Cantidades. Para ello se palnteará la siguiente situación.

Suponga que una empresa informática se dedica a la venta de computadores y actualmente no cuenta con un modelo de inventario óptimo. En estos momentos trata de determinar cómo minimizar los costos anuales relacionados con la compra de tarjetas de video para los computadores. Cada vez que se hace un pedido se incurre en un costo de $20. El precio de las taretas depende del número pedido de ellas. Si el costo anual de almacenamiento es de 20% del valor de inventario y la empresa demanda 80 tarjetas al mes, ¿cuál es la cantidad óptima de pedido? ¿cuál es el Costo Total Anual mínimo? ¿Cuál es la cantidad óptima anual? y ¿cuál es el período por pedido según las cantidades anuales?

Este tipo de situación es común cuando se compra al por mayor, para esto se debe analizar según los parámetros del modelo EOQ.

La siguiente tabla muestra los descuentos según el volumen pedido:

A partir de lo anterior se analizan las cantidades óptimas por pedido (se asume que no se aceptan faltantes) para cada descuento, siempre y cuando se tenga en cuenta lo siguiente:

- La cantidad óptima de pedido será aquella que, al momento de calcular las cantidades a partir del modelo adecuado y según los costos unitarios de cada descuento, este valor se halle dentro del rango de cantidades especificado (en la tabla, la primera columna). Caso contrario, si dicho valor no se encuentra en su rango especificado, se dice que No Cumple para el período, y la cantidad óptima será el valor más cercano a su límite de especificación.

Los datos conocidos son:

Cp = $20/pedido

Cmi = 20% Cu

d = 80 tarj/mes * 12meses/1año = 960 tajertas/año

Así, se procede en primera instancia a calcular las cantidades óptimas para cada rango especificado en la tabla, esto es:

Los comentarios en paréntesis están relacionados al criterio antes señalado, y nos permite concluir que la cantidad óptima de pedido en un período es de 139 tarjetas de video.

No obstante, no siempre la cantidad óptima de pedido para un período representa la cantidad que minimiza los Costos Totales Anuales. Recordemos que la cantidad óptima de pedido sólo permite que los costos de pedir y de mantener en inventario sean iguales, y si el costo unitario es constante, esta llega a ser la cantidad adecuada para optimizar. Pero, en esta situación, la variación de los costos unitarios generan un segundo enfoque, ya que dependerá principalmente de la relación cantidad-precio unitario. Con base en ello debe resolver la función CTA para las tres cantidades óptimas optenidas anteriormente. Esto es:

Así tendremos que:

A partir de los resultados obtenidos, podrmos apreciar que el Costo Total Anual mínimo es el incurrido cuando se toman pedidos de 300 tarjetas y es de $9766,00.

Por otro lado, analizando el comportamiento de los costos nos podemos dar cuenta que:

- A medida que se pide una cantidad mayor la diferencia entre los costos de pedir y de mantener en inventario es cada vez más grande, siendo los costos de mantener por obvias razones la que aumente y de pedir el que disminuye.

Finalmente, conociendo la Cantidad óptima anual, podemos determinar el período para cuando son más de un pedido. Así tendremos que:

Como se pudo apreciar, el modelo de EOQ con Descuentos por Cantidades representa una herramienta útil cuando existe un porcentaje de reducción en el costo unitario de los artículos que se ordenan. Análogamente al EOQ con y sin faltantes, se manejan los mismos parámetros de evaluación, la diferencia radica en que se debe hacer un análisis para cada uno de los precios unitarios especificados por el proveedor tanto para establecer la cantidad óptima en un pedido, como para establecer la cantidad óptima anual y los Costos Totales Anuales mínimos, siendo los últimos los más representativos para cualquier organización.

PUNTO DE REORDEN

El punto de Reorden r es un factor que sirve para garantizar que el de inventario manejado por la empresa en el almacen satisfaga el nivel de servicio al cliente. Para esto se debe tener en cuenta un Stock o inventario de seguridad dado por un factor estocàstico definido como:

Donde sigma t representa la desviación estándar del producto en el tiempo de entrega o:

Cuando no se conoce la desviaión del tiempo de entrega, o no son iguales los períodos dados de la demanda y del tiempo de entrega, se resuelve diviendo ambos períodos como se mostró en la anterior ecuación.

Este ùltimo se usa para cubrir las variaciones en la demanda, ademàs de prever situaciones tales como: faltas del proveedor, mal manejo de materiales, etc. Además de ello representan niveles de inventario que cubran la variabilidad de la demanda, así como ajustar las demás variables de manera que se vuelvan irrelevantes. A pesar de ello, la mayor incertidumbre es causada por los clientes debido a que sus requerimientos son difíciles de predecir.

La fórmula de Punto de reorden se muestra a continuación:

Ejemplo:

A partir de los siguientes parámetros estocástico de la demanda de focos, una empresa decide definir un Punto de Reorden adecuado para cumplir con los requerimientos de sus clientes.

La demanda en 1 semana presenta una distribución gaussiana de media 154 focos/semana y desviación estándar de 25 Focos/semana.

En primera instancia calculamos el EOQ con la demanda semanal promedio 154 focos. Entonces tendremos que:

No obstante, hay que tener en cuenta que estas unidades sólo suplen la media de la demanda, es decir el percentil de 50%. Pero ello quiere decir que no tendremos existencias para suplir aquellas que superen el valor medio.

El director de Operaciones de la empresa sugiere la política de permitir que sólo fallen en 1 pedido. Entonces debemos determinar el número de pedidos ideal. Esto es:

Ahora, considerando la política optada tendremos que el nivel de significancia será:

A partir de lo anterior tendremos que el Punto de 

La empresa debe encargar a su proveedor cada vez que haya sólo 195 unidades en almacen.

Modelo de compra sin déficit

Para trabajar este modelo se supone una tasa de producción continua, lo cual permite hacer una reposición del inventario constante durante el tiempo de producción. En este modelo en particular, por ser de compra, se deduce que el artículo no será producido sino comprado o que se necesita un material auxiliar utilizado en la producción, pero este elemento es comprado.

Este modelo es también conocido como modelo de cantidad de pedido económico o lote económico (EOQ); es uno de los modelos de inventario más antiguo y conocido; está basado en hipótesis.

Está basado en las siguientes hipótesis:

• La demanda es constante y conocida.
• El plazo de entrega es constante y conocido.
• El pedido llega en un solo lote y todo de una vez.
• Los costos por ordenar un pedido y los costos de mantenimiento son constantes y conocidos.
• No son posibles los descuentos por cantidad.
• Se evitan las roturas de inventario.
• No se permite diferir demanda al futuro.

Con estas hipótesis de la utilización del inventario a través del tiempo, el gráfico tiene forma de dientes de sierra.

Para trabajar este modelo es necesario conocer algunas variables como:

Q = Cantidad óptima a comprar por pedido (EOQ).
D = Demanda por unidad de tiempo.
Co = Costo por ordenar el pedido.
Cm = Costo de mantener una unidad por año.
CTO = Costo total por ordenar un pedido.
CTM = Costo total de mantenimiento.
CT = Costo total del inventario.

La cantidad óptima de pedido ocurrirá en el punto en que el costo por ordenar un pedido y los costos de almacenamiento sean iguales.

Costo total por ordenar	= (Demanda anual / Cantidad optima) * Costo por ordenar CTO = (D / Q) * Co
Costo total de mantenimiento	= (Cantidad optima / 2) * Costo de mantenimiento CTM = (Q/2) * Cm

Luego se procede a la igualación:

CTO=CTM

(D/Q)*Co=(Q/2)*Cm

2(D*Co)=Q(Q*Cm)

2DCo=Q^2 CM

Q^2=2DCMo/cM

Q=√(2DCo/Cm)

Ejemplo

La empresa manufacturera Galey compra 8.000 chip cada año para utilizar en los equipos que produce. El costo unitario de cada chip es de $30.000 y el costo de mantener o almacenar un chip en inventario por año es de $3.000, además se sabe que realizar un pedido tiene un costo de $10.000. ¿Cuál es la cantidad óptima de pedido?

Solución:

La información entregada por la Empresa Galey es la siguiente:

Demanda por unidad de tiempo     D = 8.000 uds/año

Costo por ordenar                          Co = $30.000 / pedido

Costo de mantenimiento                Cm = $3.000 /uds/año

Primero se debe observar que los datos a trabajar estén en la misma unidad de tiempo. Si la demanda es diaria se multiplica por el número de días que la empresa labora; cuando no se indican se asumen 20 días de producción al mes. Si la demanda es semanal se multiplica por el número de semanas a laborar en el año, normalmente está entre 50 y 52; si la demanda es semestral se multiplica por dos por cuanto el año tiene 2 semestres y así sucesivamente con otras demandas dadas en diferentes cronologías. Para el caso planteado de la empresa Galey, esta trabaja anualmente, lo que permite directamente aplicar la fórmula entregada por el modelo:

Q = √(2DCo/Cm)

Q = √ [(2(8.000)(30.000))/(3.000)]

Q =   400  uds/pedido